Counting Fish — Point Processes, the Coefficient of Variation, and the Fano Factor
Errata (21 June 2023): I erroneously stated that the mean and standard deviation of an exponential random variable with rate \(\lambda\) are both \(\lambda\). They are of course both \(1 / \lambda\).
I finally got around to reading Burstiness and Memory in Complex Systems out of Barabási's lab.
This lead me to looking up both the coefficient of variation, which the paper uses as the numerical measure for the burstiness of a point process, and a closely related quantity, the Fano factor. A quick Google search turns up a few hits, but none of them are particularly illuminating compared to the picture I have formed in my head1.
So here's that picture2.
We'll begin with the story about the homogeneous Poisson process. I've already written about it elsewhere, so I won't rehash a lot of the details here. The main thing to know about the Poisson process is that:
It's a counting process. That is, the stochastic process \((N(t))_{t \in \mathbb{R}^{+}}\) takes on values in \(\mathbb{N}\), which we can think of as the number of 'counts' of some occurrence from time 0 to time \(t\). Think of the number of particles of radiation emitted by an atom, or the number of horse-related deaths in the Prussian army over time.
The times at which a count occurs, i.e. those times \(t\) when \(N(t)\) makes a jump, are themselves random. Let's call those random jump / count times \(T_{0}, T_{1}, \ldots, T_{N-1}.\)
The picture to have in your head looks something like this:
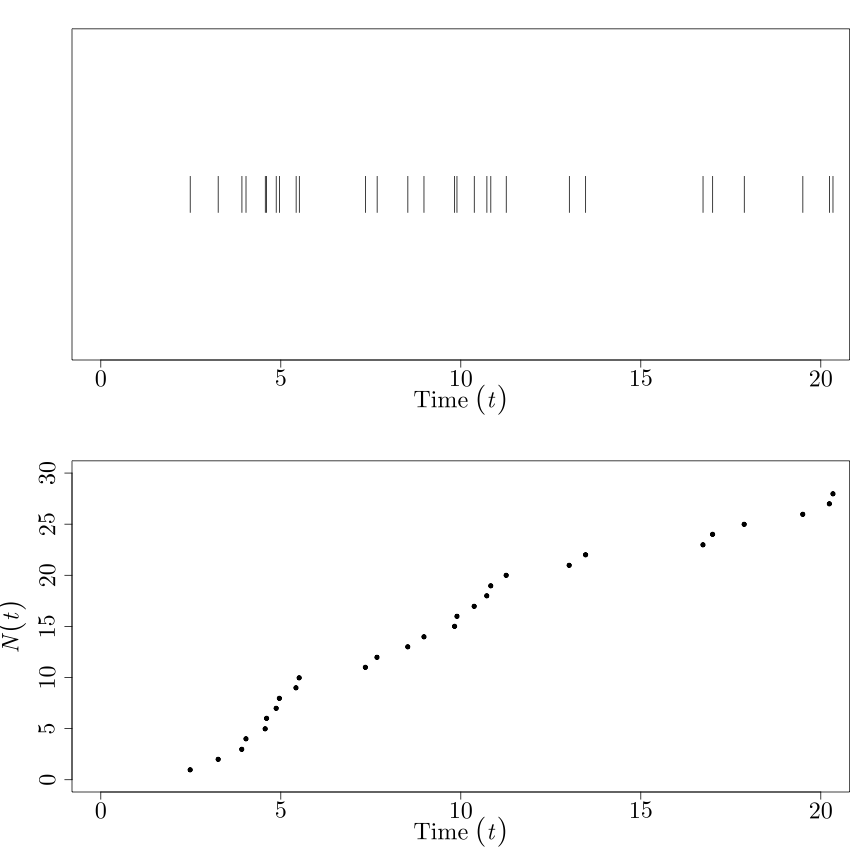
where the occurrences are on the top, and the count process \(N(t)\) is on the bottom. (\(N(t)\) should be piecewise constant, since it's defined for all \(t \in \mathbb{R}^{+}\). But I'm in a rush.)
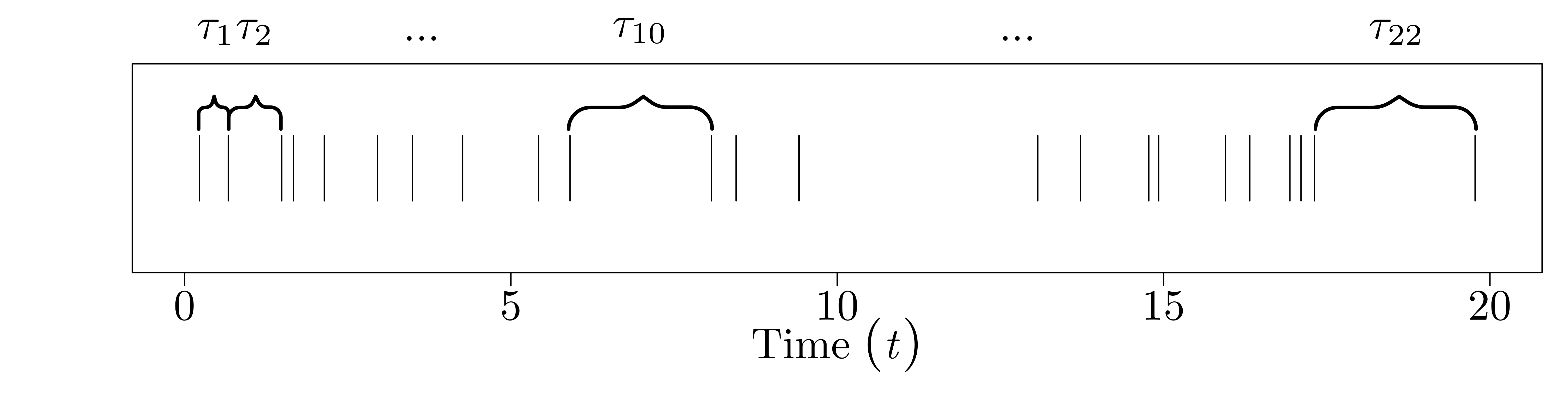
Since \(T_{i-1}\) and \(T_{i}\) are random, so is the time between them, \(\tau_{i} = T_{i} - T_{i-1}\). I'll call this the interarrival time (since it's the time between two 'arrivals'). Not only is it random, but for the Poisson process, we define the \(\tau_{i}\) to be iid exponential, with rate parameter \(\lambda\). That is, \(\tau_{0}, \ldots, \tau_{N-1} \stackrel{\text{iid}}{\sim} \text{Exp}(\lambda).\)
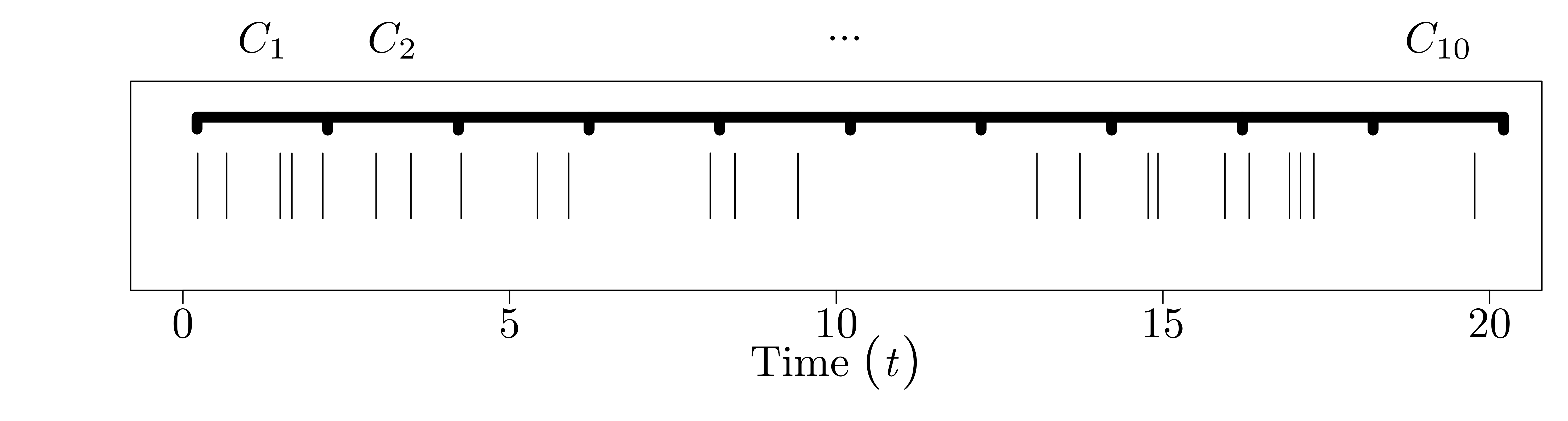
Since the counts occur at random times, the number of counts in a time interval \([(i - 1)\Delta, i \Delta]\) of length \(\Delta\) is also random. Call this value \(C_{i}\). Again, for the Poisson process, we specify that the number of counts in disjoint intervals of length \(\Delta\) are iid Poisson with rate parameter \(\Delta \lambda\). That is, \(C_{0}, \ldots, C_{N-1} \stackrel{\text{iid}}{\sim} \text{Poisson}(\Delta \lambda).\)
The picture for the interarrival times looks like this:
And the picture for the binned counts looks like this:
Now we have everything we need to define the coefficient of variation and the Fano factor, which basically correspond to how 'bursty' the process is from either the interarrival perspective or the count perspective. The coefficient of variation is about the shape of the interarrival time distribution, in particular how its standard deviation relates to its mean: \[\text{CoV} = \frac{\sqrt{\text{Var}(\tau)}}{E[\tau]}.\] Then the Fano factor is about the shape of the binned count distribution, in particular how its variance relates to its mean: \[\text{FF} = \frac{\text{Var}(C)}{E[C]}.\] Both of these ratios measure how 'clumpy' the count process is. For the coefficient of variation, this is direct: if the standard deviation of the interarrival times is much larger than the mean of the interarrival times, this means that we generally expect the occurrence times to be close together ('on average'), but that occasionally we should get large gaps between consecutive occurrences, which is what allows us to define 'bursts.' For the Fano factor, the clumpiness idea works out as so: if the expected number occurrences in a bin is small compared to the variation in the counts in a bin, then we must have a few bins that captured a lot of occurrences, and thus bursts / clumps occurred in those bins.
For a Poisson process, both the coefficient of variation and the Fano factor are 1, since an exponential random variable with rate parameter \(\lambda\) has both mean and standard deviation \(1 / \lambda\), and a Poisson random variable with rate parameter \(\Delta \lambda\) has mean and variance \(\Delta \lambda\). This is, of course, a necessary but not sufficient condition for a process to be Poisson. We are only considering the first two moments, after all. For instance, you could construct a non-Poissonian counting process whose interarrival distribution has its mean equal to its standard deviation, while still not being exponential. (Exercise: construct such a process!)
Neither the coefficient of variation nor the Fano factor is particularly mysterious when we stop to clarify what they're actually quantifying. The confusion comes when we forget to distinguish between sample and population values. But that's what 'statisticians do it better.'
The Wikipedia article on the Fano factor was clearly written by a physicist. Which seems appropriate, given that Ugo Fano was a physicist. And not to be confused with Robert Fano, who did a great deal of work in information theory. (Not that I'd ever make that mistake.)↩
I keep using the word 'picture' deliberately. I have convinced myself that mathematicians (and scientists) should, when possible, show rather than tell. I'm reminded of this quote by Richard Feynman: "I had a scheme, which I still use today when somebody is explaining something that I'm trying to understand: I keep making up examples. For instance, the mathematicians would come in with a terrific theorem, and they're all excited. As they're telling me the conditions of the theorem, I construct something which fits all the conditions. You know, you have a set (one ball) - disjoint (two balls). Then the balls turn colors, grow hairs, or whatever, in my head as they put more conditions on. Finally they state the theorem, which is some dumb thing about the ball which isn't true for my hairy green ball thing, so I say, 'False!'"↩