We consider a random vector \(\mathbf{X} = (X_{1}, \ldots, X_{N_{v}}) \in \{ 0, 1\}^{N_{v}}\). The use of \(N_{v}\) for the number of random variables in our vector is suggestive. In fact, \(\mathbf{X}\) is a Markov Random Field with \(N_{v}\) vertices. We'll assume that the probability mass function for \(\mathbf{X}\) is given by
\[ p(\mathbf{x}; \boldsymbol{\Theta}, \boldsymbol{\theta}_{0}) = \frac{1}{Z} \text{exp} \left \{ \sum_{j} \theta_{0j} x_{j} + \sum_{(j, k) \in \mathcal{E}} \theta_{jk} x_{j} x_{k} \right \}, \]
where \(\mathcal{E}\) is an edge list, with \((j,k) \in \mathcal{E}\) only if there exists an edge between random variable \(j\) and random variable \(k\). (Remember that we implicitly have a Markov Random Field in the background, so we also have an undirected graphical model with nodes and (undirected) edges.)
Borrowing from our physicist friends, the joint mass function can be rewritten in a much more compact form using matrix/vector notation as
\[ p(\mathbf{x}; \boldsymbol{\Theta}, \boldsymbol{\theta}_{0}) = \frac{1}{Z} \text{exp} \left \{ \boldsymbol{\theta}^{T}_{0} \mathbf{x} + \frac{1}{2} \mathbf{x}^{T}\boldsymbol{\Theta} \mathbf{x} \right \} = \frac{1}{Z} \text{exp} \left \{ E(\mathbf{x}; \boldsymbol{\Theta}, \boldsymbol{\theta}_{0}) \right \}.\]
Again, the \(E\) here should be suggestive. We can think of this as some sort of energy function of \(\mathbf{x}\). We can do this, but we won't, for now. I'm writing down a particular statistical model. We'll see some of the consequences of that model later. I warned you that my first language is statistics.
You'll notice the \(\frac{1}{Z}\) out front of our probability mass function. It's there to make sure that our sum over all \(\mathbf{x} \in \{ 0, 1\}^{N_{v}}\) gives us 1, as it must. That is, it's a normalization constant. Physicists have a different name for it: they call it the partition function. It gets a fancier name in statistical mechanics because, when a distribution takes a form like \(p(\mathbf{x}; \boldsymbol{\Theta}, \boldsymbol{\theta}_{0})\) above, you can derive certain properties of \(p\) by manipulations with the partition functions (taking logs, derivatives, etc.). For completeness, the partition function is
\[ Z = \sum_{\mathbf{y} \in \{ 0, 1\}^{N_{v}}} \text{exp} \left \{ E(\mathbf{y}; \boldsymbol{\Theta}, \boldsymbol{\theta}_{0}) \right \}\]
where we introduce a dummy summation variable \(\mathbf{y}\) here so as not to confuse ourselves with the \(\mathbf{x}\) showing up as the argument to \(p(\mathbf{x}; \boldsymbol{\Theta}, \boldsymbol{\theta}_{0})\).
And with that, we're done. We've fully specified this particular model, since we can compute anything we might possibly want to know about \(\mathbf{X}\) using \(p(\mathbf{x}; \boldsymbol{\Theta}, \boldsymbol{\theta}_{0})\). For instance, we might want to compute it's mean value, in which case for each \(X_{j}\) in \(\mathbf{X}\), we would compute
\[ E[X_{j}] = \sum_{\mathbf{x} \in \{ 0, 1\}^{N_{v}}} p(\mathbf{x}; \boldsymbol{\Theta}, \boldsymbol{\theta}_{0}) x_{j}, \]
collect those together into a vector, and we would have \(E[\mathbf{X}]\). The same goes for the covariance matrix, etc. We're not really done, since to compute any of these things, we'll have to sum over a (possibly) very large set \(\{ 0, 1\}^{N_{v}}\). This set has cardinality \(2^{N_{v}}\), which grows exponentially in \(N_{v}\). That's bad news for computational tractability.
But fortunately, being statisticians, we can get around this by sampling from \(p(\mathbf{x}; \boldsymbol{\Theta}, \boldsymbol{\theta}_{0})\). Or, as it's usually called in this context, using Monte Carlo methods. We can approximate any expectation by drawing a random sample \(\mathbf{X}^{(1)}, \mathbf{X}^{(2)}, \ldots, \mathbf{X}^{(N)}\) from \(p(\mathbf{x}; \boldsymbol{\Theta}, \boldsymbol{\theta}_{0})\) and computing
\[ E[g(\mathbf{X})] \approx \frac{1}{N} \sum_{i = 1}^{N} g(\mathbf{X}^{(i)}).\]
By the law of large numbers, our sample average will converge on the true average, and we're done.
Of course, how we sample from \(p(\mathbf{x}; \boldsymbol{\Theta}, \boldsymbol{\theta}_{0})\) is an another question. A standard approach is to use Gibbs sampling. Gibbs sampling, in essence, generates a sample from a multivariate distribution by successively sampling from its conditional distributions. That is, it's easy to show that for a fixed \(X_{j}\), the conditional distribution, conditioning on all other \(X_{k}\) making up \(\mathbf{X}\), is
\[ P(X_{j} = 1 \ | \ \mathbf{X}_{-j} = \mathbf{x}_{-j}) = \frac{1}{1 + \text{exp} \left\{ - \theta_{j} - \sum_{(j, k) \in \mathcal{E}} \theta_{k} x_{k}\right\} } \]
where \(\mathbf{X}_{-j} = (X_{1}, \ldots, X_{j-1}, X_{j+1}, \ldots, X_{N_{v}})\) is the random vector once we've removed the random variable of interest \(X_{j}\). Since, given \(\mathbf{X}_{-j}\), this distribution is easy to sample from, we just iterate through all of the \(j\), successively updating the value of \(X_{j}\) based on this probability. The succession of \(\mathbf{X}^{(i)}\) that we get out of this sampling approach forms a Markov chain whose stationary distribution is \(p(\mathbf{x}; \boldsymbol{\Theta},\boldsymbol{\theta}_{0})\). So if we wait long enough, doing this sampling is basically the same as sampling from \(p(\mathbf{x}; \boldsymbol{\Theta}, \boldsymbol{\theta}_{0})\).
Let's wrap up by seeing why we might want to compute an expectation. Recall that the log-likelihood for a sample \(\mathbf{X}^{(1)}, \mathbf{X}^{(2)}, \ldots, \mathbf{X}^{(N)}\) is
\[ \ell(\boldsymbol{\Theta}, \boldsymbol{\theta}_{0}; \mathbf{X}^{(1)}, \ldots, \mathbf{X}^{(N)}) = \sum_{i = 1}^{N} \log p(\mathbf{X}^{(i)} ; \boldsymbol{\Theta}, \boldsymbol{\theta}_{0}).\]
If we want to do optimization (maximize the log-likelihood), we need to take the gradient of \(\ell(\boldsymbol{\Theta}, \boldsymbol{\theta}_{0}; \mathbf{X}^{(1)}, \ldots, \mathbf{X}^{(N)})\) with respect to \((\boldsymbol{\Theta}, \boldsymbol{\theta}_{0})\). A little calculus shows that
\[ \frac{1}{N} \frac{ \partial}{\partial \theta_{jk}} \ell(\boldsymbol{\Theta}, \boldsymbol{\theta}_{0}; \mathbf{X}^{(1)}, \ldots, \mathbf{X}^{(N)}) = \frac{1}{N}\sum_{i = 1}^{N} X^{i}_{j} X^{i}_{k} - E_{(\boldsymbol{\Theta}, \boldsymbol{\theta}_{0})}[X_{j} X_{k}]\]
where the subscript on the expectation reminds us that we're taking the expectation with the parameters set to \((\boldsymbol{\Theta}, \boldsymbol{\theta}_{0}).\) Thus, the gradient is the sample correlation minus the population correlation, and our goal in maximum likelihood estimation is to drive this difference to zero. (Recalling that, if a maxima exists on the interior of our parameter space, we want to the gradient to equal the zero vector.) This (almost) sheds light on the quotation from the Quanta article:
The synapses in the network start out with a random distribution of weights, and the weights are gradually tweaked according to a remarkably simple procedure: The neural firing pattern generated while the machine is being fed data (such as images or sounds) is compared with random firing activity that occurs while the input is turned off.
To get at that, we'd have to introduce latent ('hidden') random variables, and go through this same procedure with the likelihood for the observed random variables. I won't do this, but you can find the derivation in Section 17.4.2 of The Elements of Statistical Learning.
Now we see why we need to compute an expectation: to get the gradient, we need to compute \(E_{(\boldsymbol{\Theta}, \boldsymbol{\theta}_{0})}[X_{j} X_{k}],\) for each edge \((j, k) \in \mathcal{E}\). This can be nigh on impossible when \(N_{v}\) takes large values (say, greater than 30). But by sampling (which is relatively inexpensive), we can get as good as an approximation as we'd like to this quantity by taking more samples. Monte Carlo 'beats' the curse of dimensionality again!
There's much more to the story of this model, which goes by the name of a 'first-order-interaction Poisson log-linear model for multi-way tables of counts' in the statistics literature. But this gives a flavor of how a statistician might think about the model and how to perform inference on it: we're learning a particular parametric model that accounts for pairwise interactions between a collection of random variables (a random field), and we learn the parameters of the model using maximum likelihood estimation with some bells and whistles thrown in because doing things with the probability mass function becomes computationally unwieldy.
Coming up, I'll attempt to talk about the model from the perspective of a machine learner / computational neuroscientist. That will be much more challenging...




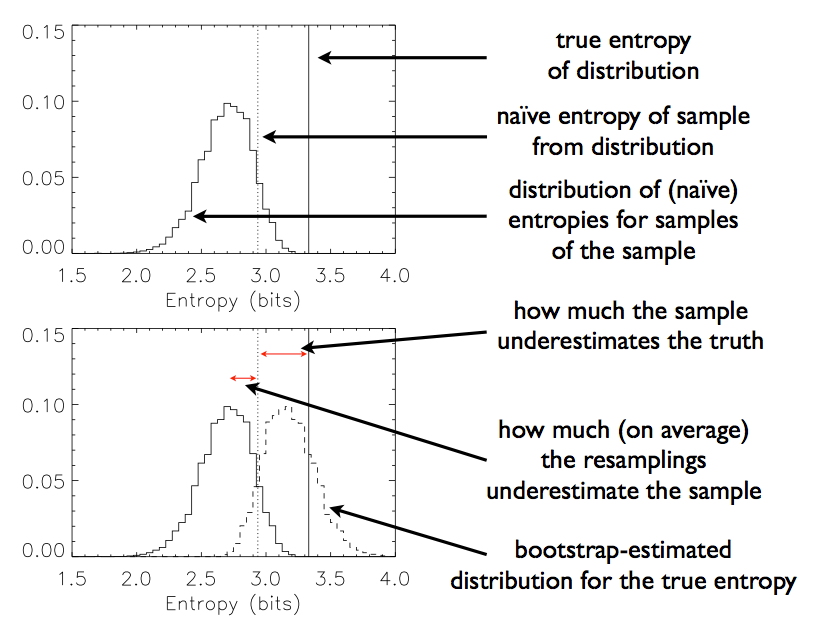









 This looks very much like a (biased) random walk, and for good reason: if we take the logarithm of a multiplicative process, it becomes an additive process, and we in fact find ourselves with a random walk. This explains the use of logarithms throughout. Logarithms also makes the computer much happier. If we shaded the lines in by the number of sample paths that traverse them, we would see that most people follow along the central trajectory, with less and less people following along the further out branches. (We see this explicitly in the most extreme trajectories, which don't get traced out with only 10000 sample paths.) We can of course compute the proportion of walks that end up at node, first for \(t = 1\)
This looks very much like a (biased) random walk, and for good reason: if we take the logarithm of a multiplicative process, it becomes an additive process, and we in fact find ourselves with a random walk. This explains the use of logarithms throughout. Logarithms also makes the computer much happier. If we shaded the lines in by the number of sample paths that traverse them, we would see that most people follow along the central trajectory, with less and less people following along the further out branches. (We see this explicitly in the most extreme trajectories, which don't get traced out with only 10000 sample paths.) We can of course compute the proportion of walks that end up at node, first for \(t = 1\)


